- 大学生のための実験理論
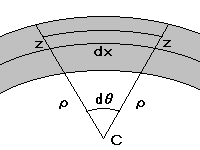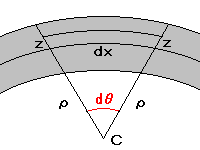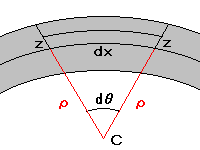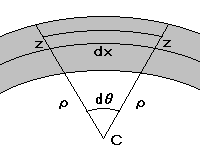
- 一様な棒をたわませた時,伸縮の無い中層 (dx) が曲率の中心 (C) を見こむ角を (dθ) とし,曲率半径を (ρ) とすれば,中層から (z) の距離にある断面 (dS) の平行層の伸びは,

- で表されるので、断面 (dS) の平行層のひずみは、
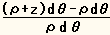 となり、これを計算すると、
となり、これを計算すると、
ひずみ=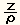 となる。
となる。
- また,この層に加わる張力を (dF) とすれば,
 であるヤング率の定義から、
であるヤング率の定義から、
 となり、これを計算して簡単にすると、
となり、これを計算して簡単にすると、
 となる。
となる。
- 断面に加わる曲げモーメント (L) は
 なので、上の (dF) を代入すると
なので、上の (dF) を代入すると
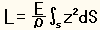 となる。
となる。
- ここで
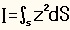 は断面 (S) が中層との交線のまわりの慣性モーメントに相当するものを表わす。
は断面 (S) が中層との交線のまわりの慣性モーメントに相当するものを表わす。
- 次に長さが (l) の片持梁の中層を考える時,一端に (M) の重りを掛けたため、(O) からの距離が (x) である (dx) の部分に相当する微小降下を (de) とすれば,

- と表わされるが,この際の曲げモーメントは,

- であるから,上二式より曲率半径 (ρ) を消去して,

- と変形する。 したがって,一端降下としては,

- と表わされるのであるが,厚さ (a) ,幅 (b) の角棒を,距離が (l) の水平支点間に支え,中央に (M) のおもりを掛けた際の中点降下としては,上式の (l) 代わりに (1/2) を,(Mg) の代わりに (Mg/2) を,
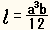 とおくことによって,中点降下 (e) を,
とおくことによって,中点降下 (e) を,

- とする。 したがって,棒のヤング率 (E) は,

- で求められる。 中点降下 (e) を,“光のてこ”の方法によって測定すれば,

- となる。 ここで (x) は鏡と尺度との距離, (Δy) はおもりによる望遠鏡の読みの移動, (z) は鏡における支点間の垂直距離である。



- ・現在位置。
- ヤング率
- →測定法
- →ユーイングの装置によるヤング率
- →実験理論
- →大学生のための実験理論
- ・参考文献
- ・物理学実験 / 吉田 卯三郎 ・ 武居 文助 ・ 橘 芳寛 ・ 武居 文雄 / 三省堂

となり、これを計算すると、
となる。
 であるヤング率の定義から、
であるヤング率の定義から、
となり、これを計算して簡単にすると、
となる。
なので、上の (dF) を代入すると
となる。
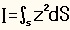 は断面 (S) が中層との交線のまわりの慣性モーメントに相当するものを表わす。
は断面 (S) が中層との交線のまわりの慣性モーメントに相当するものを表わす。
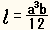 とおくことによって,中点降下 (e) を,
とおくことによって,中点降下 (e) を,




となり、これを計算すると、
となる。
 であるヤング率の定義から、
であるヤング率の定義から、
となり、これを計算して簡単にすると、
となる。
なので、上の (dF) を代入すると
となる。
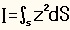 は断面 (S) が中層との交線のまわりの慣性モーメントに相当するものを表わす。
は断面 (S) が中層との交線のまわりの慣性モーメントに相当するものを表わす。
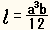 とおくことによって,中点降下 (e) を,
とおくことによって,中点降下 (e) を,


